문제 요약
매일 아침, 세준이는 학교에 가기 위해서 차를 타고 D킬로미터 길이의 고속도로를 지난다. 이 고속도로는 심각하게 커브가 많아서 정말 운전하기도 힘들다. 어느 날, 세준이는 이 고속도로에 지름길이 존재한다는 것을 알게 되었다. 모든 지름길은 일방통행이고, 고속도로를 역주행할 수는 없다.
세준이가 운전해야 하는 거리의 최솟값을 출력하시오.
문제 분석
지름길 객체를 만들어 시작, 끝, 길이를 저장해 준 뒤 이를 시작위치를 기준으로 정렬해 준다.
이후 DP배열을 만들고 이를 고속도로 기준으로 채워나가면서 지름길 적용이 가능하게 되면, 지름길을 적용해 준다.
ex) 다음 예제의 경우
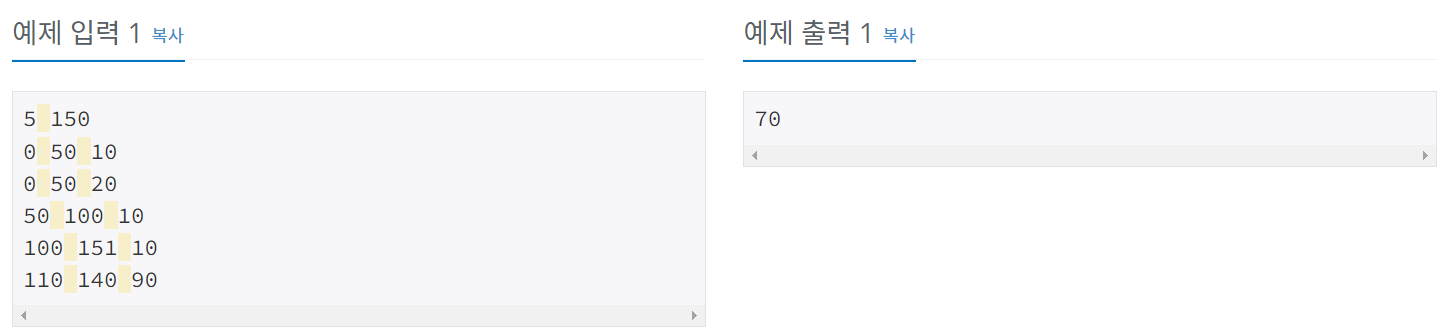
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;
public class Main {
static class Shortcut implements Comparable<Shortcut> {
int start;
int end;
int dist;
public Shortcut(int start, int end, int dist) {
this.start = start;
this.end = end;
this.dist = dist;
}
@Override
public int compareTo(Shortcut o) {
return this.start - o.start;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 지름길 개수
int N = Integer.parseInt((st.nextToken()));
// 고속도로 길이
int D = Integer.parseInt((st.nextToken()));
// 지름길 정보를 저장할 배열
Shortcut[] shortcuts = new Shortcut[N];
for(int i = 0; i < N; i++){
st = new StringTokenizer(br.readLine());
shortcuts[i] = new Shortcut(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
}
// 시작위치를 기준으로 지름길 정렬
Arrays.sort(shortcuts);
// 각 위치까지의 최소거리를 저장할 DP배열
int[] dp = new int[D+1];
for(int i = 1; i <= D; i++){
// 기본적으로 이전 위치에서 1만큼 더 거리를 더함 (고속도로를 그대로 갈 경우)
dp[i] = dp[i-1] + 1;
// 이제 모든 지름길을 확인해본 뒤 가능한게 있다면 갱신해보자.
for(Shortcut s : shortcuts) {
// 지름길 끝 위치가 현재 위치와 같다면?
if(s.end == i){
// 현재 위치까지의 최소 거리와 (지름길의 시작 위치까지의 거리 + 지름길의 거리) 중 작은 것을 선택
dp[i] = Math.min(dp[i], dp[s.start] + s.dist);
}
}
}
System.out.println(dp[D]);
}
}정리
새로 배운 내용
없음
개선할 점
다익스트라를 사용해서 풀 수 있는 문제 같은데, 어떻게 풀어야 할지 모르겠어서 이렇게 풀었다.
정렬 순서를 변경하면 좀 더 시간 최적화가 가능하지 않을까?
더 찾아볼만한 사항
다익스트라로도 풀어보자.
'알고리즘 풀이 > 백준' 카테고리의 다른 글
| [Gold IV] 비슷한 단어 - 2179 (Java) (0) | 2023.07.12 |
|---|---|
| [Silver I] 카드 합체 놀이 - 15903 (Java) (0) | 2023.07.11 |
| [Gold IV] 공유기 설치 - 2110 (Java) (0) | 2023.07.05 |
| [Gold V] A와 B 2 - 12919 (Java) (0) | 2023.07.05 |
| [Silver IV] 점화식 - 13699 (JAVA) (0) | 2023.07.03 |




